帯分数の四則演算の解き方 足し算の解き方 帯分数の足し算については、通常の分数の足し算でも重要になる"通分"や帯分数の基本である「\(1\dfrac {2}{3}\)が\(1\dfrac {2}{3}\)であること」などが理解できていれば問題なく計算できるはずです。 では具体的に計算方法について見ていきましょう。求め方は全く変わらないので安心してください。 しかも、アルファベットで書くとかっこよく見えます。 それでは、 を求める計算をまとめます。 まとめ を求める計算を解くときは 計算の順序は普段と逆; 逆算の解き方 基本は3ステップです。 手順1まずは計算の順序を考えてみましょう。 逆算ではなく、普通の計算の順序で、+-×÷に番号を付けます。
四則混合の計算問題に強くなろう 家庭で教える算数 中学受験ナビ
四則混合計算 解き方 分数
四則混合計算 解き方 分数- 分数や小数だと、必ずしも大きい方÷小さい方とは限りません。 - 、÷ ときは、前-後、前÷後です。 そして、大事なところなのでもう一度。 ③小数、分数の変換 もうひとつは小数、分数の四則混合特有の問題です。 分数の四則混合の計算で、先に計算の仕方を決めてから計算する習慣を、高いレベルまで育てることができます。 育てる旅が続きます。 より複雑な計算の仕方になります。 より複雑なガイドになります。 さらに育てます。 +・-・×・÷ のある四則混合です。 別々の余白で計算すると決めます。 かっこの外の × が、4番目の計算です。 別々の余白で計算する
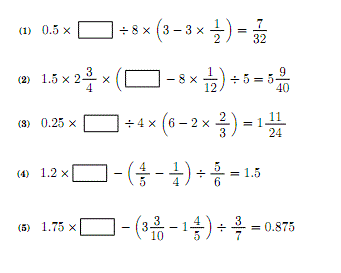



かみのドリル 逆算ドリル 小数 分数
小数を分数に変換する方法 それでは、小数を分数に変換する方法を確認しておきましょう!とっても簡単なことですよ (^^) 考え方としてはこんな感じです。 $$\Large {03=3\div 10=\frac {3} {10}}$$ 03というのは3から小数点を左に1つ 加減算と乗除算の次は、これらが混在する四則混合算です。 この四則混合算をこなせるようになるのが、計算問題での最終目標です。 四則4年 式と計算の順じょ 2/2ページ 子どもの学習支援 by いっちに算数 スマホ版 ※先生用の補足は次ページに掲載しています。 たし算・ひき算・かけ算・わり算が混じった式の計算を四則混合計算といいます。 教え方3四則計算8(分数) 次の計算をせよ。 4(2 1 3 )÷( 7 3 ) 8 5 ( 5 3 2)×( 6 5 ) 4( 3 2 7 3 )÷ 1 12 7( 1 3 5 4 )×(12) 2 3 ( 4 3 9 2 )×( 2 7 ) 11 2 ( 1 4 7 3 )÷ 5 6 14 3 ( 7 3 9 5 )×( 5 8 ) 11 7 ( 9 7 5 3 )÷ 8 9
四則混合 基礎(整数のみ) 全5ページ(3回分) 基礎・1回目; 四則混合算の解き方は以下の2つです。 (1) ()内を先に計算する。 (2) 掛け算、割り算を先に計算する。 中学数学|正負の数の四則混合算を解いてみよう 加減算と乗除算の次は、これらが混在する四則混合算です。 この四則混合算をこなせるようになるのが、計算問題での最終目標です。 四則混合算が解ける頃には、多項式や単項式の区別がつき、計算の
四則計算6(分数) 次の計算をせよ。 1 2(2)× 3 41 4 3 ÷(8 3)1 3 (3 2)×45 2(4 7)÷(8 7)7 5 (2)× 3 5 13 418 5 ÷ 9 107 6(8 9)× 3 4 3 4 9 10 ÷(18 5) 次の計算をせよ。 7 9(4 5)×(10 3)5 4 9 28 ÷(3 14)11 6 (1 3)× 5 2 2 3(9 10)÷(3 5)13 4(7 3)× 9 14 5 127 ÷ 9 105 6(6 7)× 21 8 7 3 12÷(9 5)現在定期テスト前の方にお勧めのコンテンツ 中1 正負の数の計算の練習問題(youtube再生リスト) 正負の数 四則混合計算 練習問題(標準レベル) – 正負の数 四則混合計算 練習問題(応用レベル) – 正負の数 解説 – チャンネル登録 中学受験用の分数の四則計算の問題プリントが 無料が沢山入手できるサイトをお教えください。 例えば下記のサイトのような感じの問題が欲しいです。 x,y∊ℝℚ, x




就活の計算ドリル 1 四則逆算 計算問題 Com 数学 Kindleストア Amazon




中学数学 正負の数 でつまずく原因と解決法 四則混合 分配法則
具体的な問題例 以上のことをふまえて次のような問題を考えてみましょう. 問題: (2×3-1)+ {÷ ( -5)+7}-2=15 まずこの問題では2×3-1が先に計算できるのでその分を先に計算してしまいます.2×3-1=5なので,この問題は 5+ {÷ ( -5)+7}-2=15 と書くことができます.少しだけ単純になりましたね. 次に計算の順番を書き込みます. 逆算なので⑤から 中3数学 平方根の利用 式の値③ 中3数学 平方根の利用 式の値③ 今回の問題はこちら x=√2+1、y=√2ー1のとき、 x^2+2xyy^2 の値を求めなさい。 解説は下にあります。 "中3数学 平方根の利用 式の値③" の 続きを読む 投稿日小数を分数になおす方法は、 $整数\div10=$ $整数\div100=$ $整数\div1000=$ と順番に計算して見つけます。 例えば小数が01の場合、 $1\div10=01$ ですから、分子に整数を、分母に割った数をつけ、 $01=\displaystyle\frac{1}{10}$ となります。 小数$021$を分数になおす場合、 $21\div10=21$ で答えが$021$になり




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
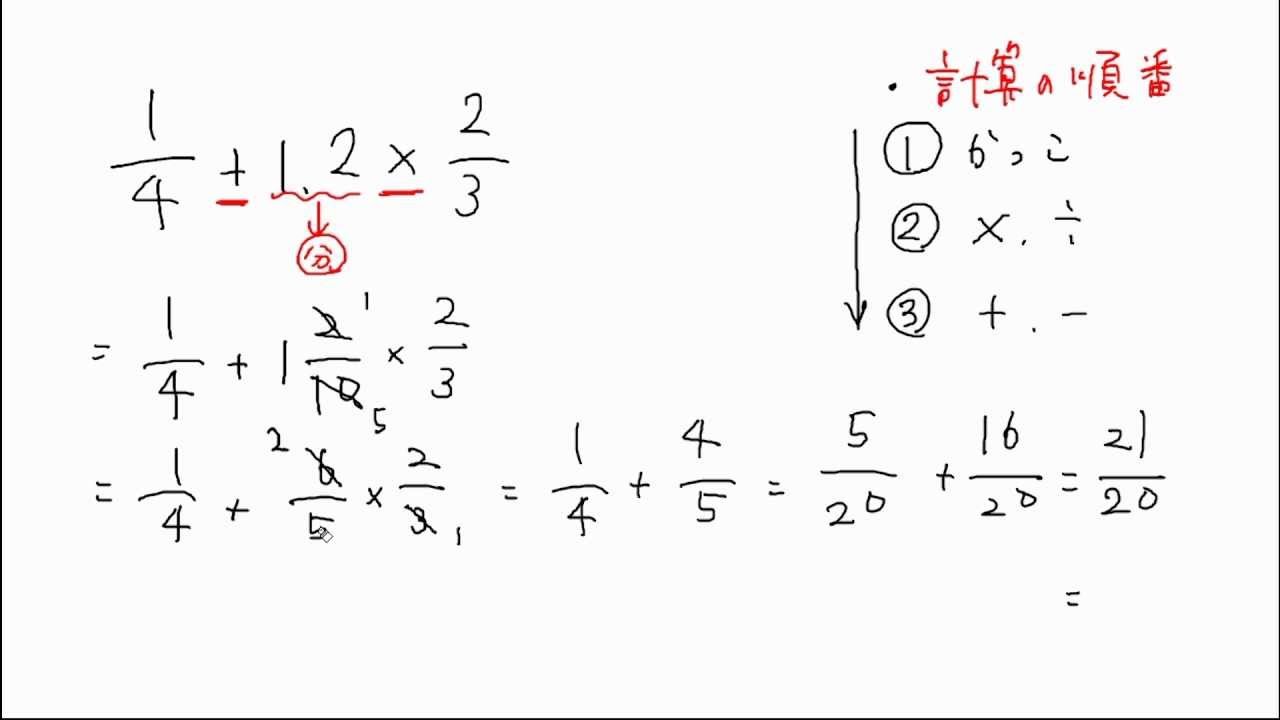



計算まとめ 四則の混じった計算1 Youtube
分数四則混合のドリル 概要 分数の四則混合です。難易度は低めで、式も短いです。 経過 09年11月1日 分数の足し算・かけ算と分数の足し算・わり算を作成しました。 09年11月2日 では、これはどうでしょう。 を求めるには 5−3=2 という計算をしなければなりません。 使われている記号は−のままなので、『−が+になっている』とは言えませんね。 2× =6 これはどうでしょう。 を求めるには6÷2=3という計算をします。 使われている記号が×から÷に変わっているので、『×が÷になっている』というのは正しいですね。 6÷ =3 では分数の乗除 分数・小数の混合計算 小数・分数の計算のまとめ 領域 小学校低学年 小学校中学年 小学校高学年 領域 中学校第1学年 中学校第2学年 中学校第3学年 正の数・負の数 ・正負の数の必要性と意味 (数の集合と四則) ・正負の数の四則計算




文字式の割り算の問題 表し方は分数で書くことが多い 中学や高校の数学の計算問題




四則演算 小数から分数への変換
まず簡単な四則計算の逆算からやり方を勉強していきましょう。 問題1 +4=12 と4を足すと12になる事から =12−4を計算すれば良いことはすぐに予想がつくと思います。 四角の位置を4と逆にしても 問題2 4+ =12 を求める式 =12−4は変わらない事から 四則混合計算〈例題〉 次の計算をしましょう。 ①8+3-5+7 ②30÷6+8×4 ③ 24-(3+5)÷4 ⑤42÷{12÷(5+1)+3×4} ⑥57-{14÷(26-19)×8}+12÷3 解き方 ①は、×も÷もかっこ( )も使われていないので、左から順番に計算していきます。 8+3の部分から計算します。分数の足し算・引き算の基本的な方法 分数の足し算・引き算の基本的な手順は以下の通り。 分数の足し算・引き算の手順 通分する(分母を揃える) 分子同士を計算する なぜ通分しなければいけないのか? たとえば分母が等しい時を考えてみると、計算は普通の足し算・引き算と同じ要領でスムーズにできるのがわかります。 分母が同じということは、同じ




新着四則混合計算 小学生 最高のぬりえ




平方根の四則混合計算 清水塾
分数とは、ある数を 0 でない他の数で割った商を、横線の上(分子)に割られる数、横線の下(分母)に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。各項目では、加減乗除の四則計算について、それぞれの計算方法と簡単な計算例をご紹介しています。分数の計算ドリル このページのドリル作成プログラムによって,次に示すような分数の2項3項の四則演算の練習問題がつくられます. 数値の大きさを調整できます.また,仮分数や帯分数もドリルに含ませることが設定に従って可能です. 例) 2 5 6 ÷ 2 帯分数の四則演算の解き方 足し算の解き方 帯分数の足し算については、通常の分数の足し算でも重要になる"通分"や帯分数の基本である「\(1\dfrac {2}{3}\)が\(1\dfrac {2}{3}\)であること」などが理解できていれば問題なく計算できるはずです。



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料




正負の数 剰余 整数 解答 046 100
すぐるゼミ・小数の四則混合問題 小数の四則混合問題 中学受験専門塾・優学習会 すぐるホームページ > すぐるゼミ > 算数 問題番号がボタンになっています。 クリックすると答えと解説が表示されます。 15× (54-14)+15 問題1の答え 7.5 ①分数をふくむ方程式の解き方(1) まず、下の方程式を見て下さい。 文字の項も数の項も、すべての項に分数がふくまれています。 分数をふくむ方程式をそのまま計算するのは、大変そうですよね。 じつは小数の方程式と同じように、分数をふくむ方程式も、 すべて整数の方程式 にするこ 分数四則混合のドリル2 概要 四則混合の続編です。少し難しい計算練習です。 経過 11年7月10日 ファイルは16枚のものと48枚のものの2通り作りました。 数値は違いますが、同じ条件で作っているのでレベルは大体同じぐらいです。




答えが2つに分かれ 海外のネット界が二分している話題の計算問題 その理由とは カラパイア




ট ইট র 正負の数 হ য শট য গ
逆算のやり方総まとめ! 中学受験やSPI対策にも 逆算を間違えてしまう中学受験生の方「苦手だから、しょうがない」と半分あきらめていませんか? 実は、たったひとつのコツをつかむだけで逆算のミスがあっという間に減るんですよ! この記事では たし算、かけ算は2つの数の順番をかえても同じ答えになります。 例えば、48は84と、7×3は3×7と同じ答えです。 これを交換の法則といいます。 たし算およびかけ算は3つの数の順番をかえても同じ答えになります。 これを結合の法則といいます。 (14)6は1 (46)と同じで答えは10です。 同様に (2×3)×8と2× (3×8)は同じ答えになります。 これらの法則を使って、数 1 つの四則混合の答えを出すために、 たし算やひき算やかけ算やわり算のように、 種類の違う分数の計算をします。 分数の違う種類の計算のそれぞれを、 「え~と、この計算は確か・・」のように、 思い出しながらではなく、 半ば習慣のようにします。



逆算の解き方 カテキョウブログ



逆算の解き方 カテキョウブログ
2 3 10 - 4 5 × 7 3 ÷2 はじめに、帯分数 2 3 10 を仮分数 23 10 に直します。 足し算・引き算よりも掛け算・割り算を先に計算するという四則演算のルール(計算の順序)があるので、引き算よりも先に 4 5 × 7 3 ÷2を計算します。 2 3 10 - 4 5 × 7 3 ÷2= 23 10 - 4 × 7 × 1 5 × 3 × 2 = 23 10 - 14 15 = 69 30 - 28 30 = 41 30 答え 41 30または111 30



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料




小数の暗算の計算プリント 2ケタと3ケタ混合の引き算 これができれば問題なし 全450問無料 算数パラダイス




2桁の3つの掛け算と足し算と引き算 問題 002 400
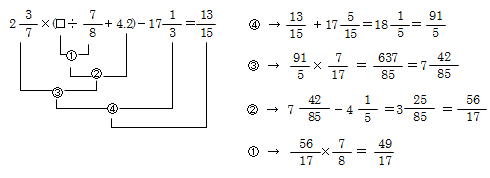



計算力の強化 前田昌宏の中学受験が楽しくなる算数塾




小学4年生の算数 のある式の計算 練習プリント 無料ダウンロード 印刷 ちびむすドリル 小学生



1




第26回 分数の計算 四則混合計算 逆算 5年生 日能研の歩き方




小学生の計算力に関する実態調査 07



3



4年算数 式と計算の順じょ 教え方のポイント 2




四則混合計算の方法は 練習問題を用いながら計算のルールやおすすめ問題集まで解説 学びtimes




第26回 分数の計算 四則混合計算 逆算 5年生 日能研の歩き方
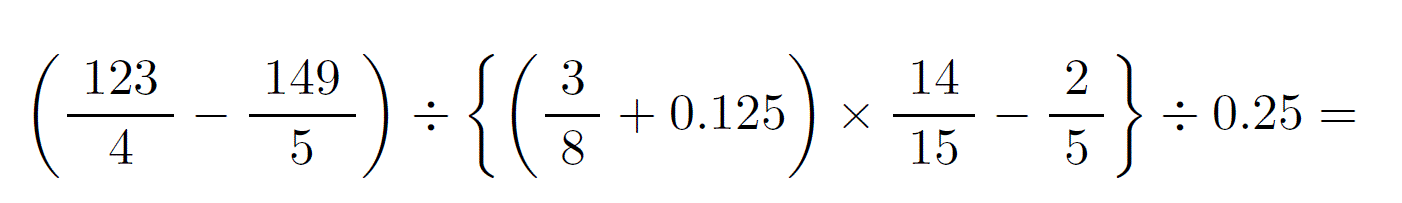



かみのドリル 中学受験算数計算 少しずつ増やしていくページ2
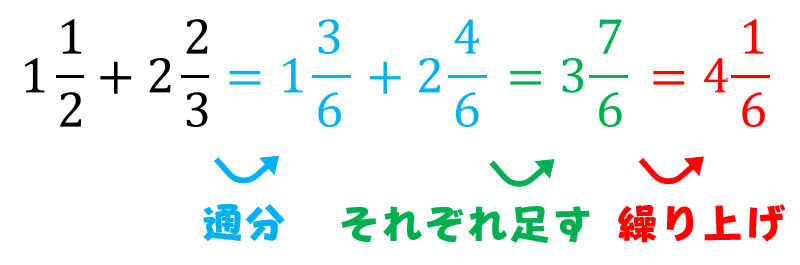



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




脳トレ計算問題 虫食い算 符号入れ 四則混合 計算問題 Com 脳トレ 就活に




四則混合計算の方法は 練習問題を用いながら計算のルールやおすすめ問題集まで解説 学びtimes
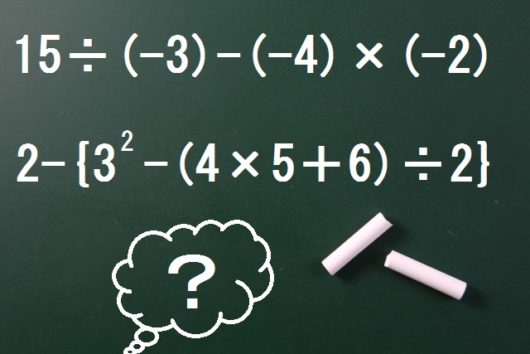



中学数学 正負の数 でつまずく原因と解決法 四則混合 分配法則



平方根 第10講 例題1 平方根の四則混合計算 清水塾




四則演算 小数から分数への変換




計算のきまりの勉強のやり方 まなびのへや




四則演算 小数から分数への変換




四則混合逆算を書き出し方式で極める



計算問題ドリル 3項の四則演算




算数 分数と小数の混じった計算方法とは 解き方を1から解説 数スタ




分数の四則計算 無料で使える学習ドリル




文章問題で四則演算の理解度をチェックする 最先端家庭学習watch
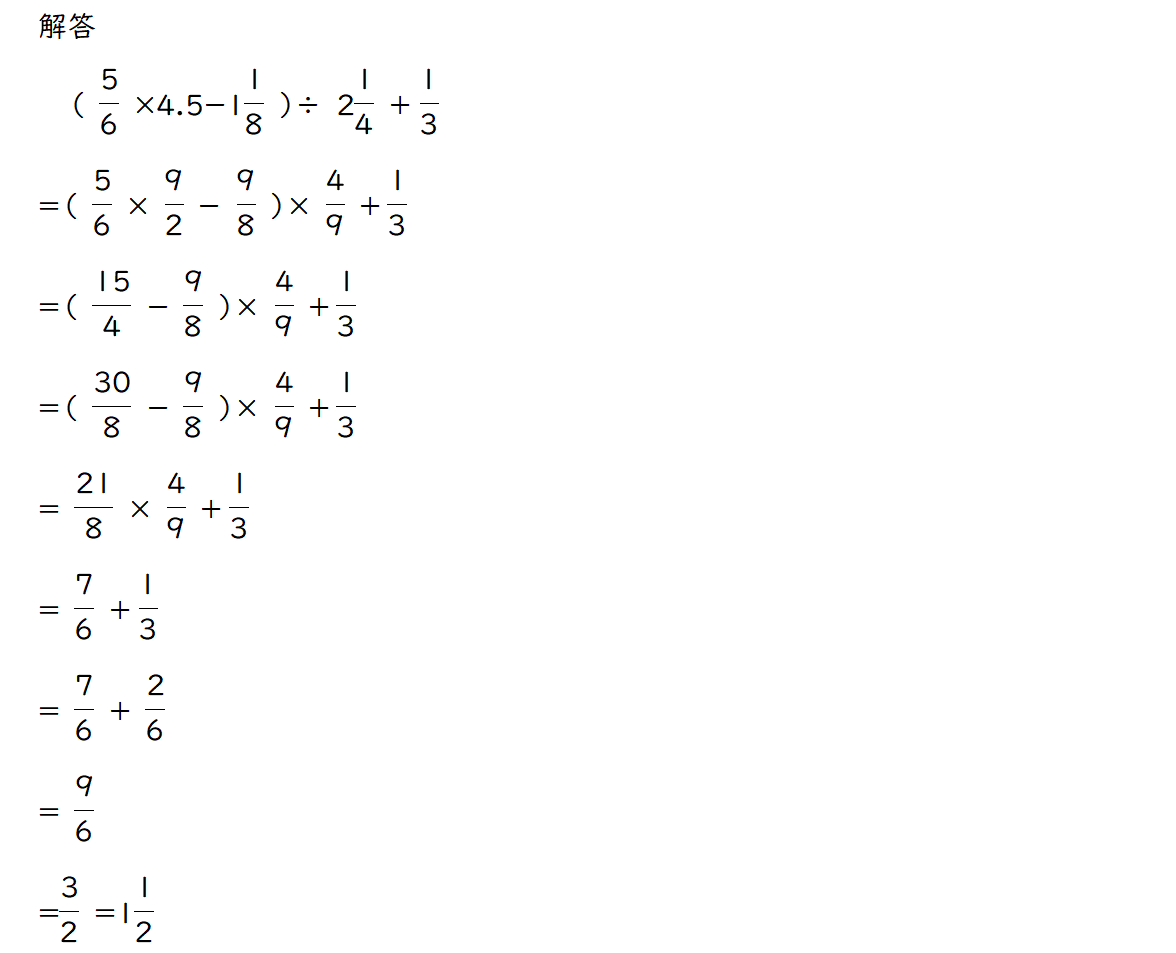



分数小数混合四則計算 東洋英和女学院 H27大問1の2




そろばん問題集 珠算問題集 朝日プリント社 try an




正負の数の計算ー四則混合 無料で使える中学学習プリント




Youtube Lesson 中1 正の数負の数 第10回 四則混合計算 難問編 桂坂数学教室




文字式の四則計算 中学1年 Youtube
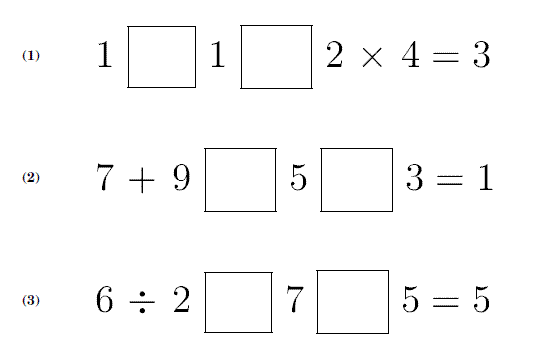



かみのドリル 四則をあてはめる算数パズル




新着四則混合計算 小学生 最高のぬりえ



中学生の数学講座 四則混合1




小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館




2桁の3つの掛け算と足し算と引き算 問題 010 400
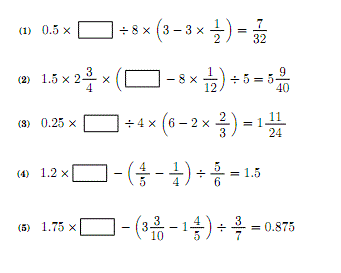



かみのドリル 逆算ドリル 小数 分数




四則演算 小数から分数への変換



四則混合の計算問題に強くなろう 家庭で教える算数 中学受験ナビ




最新のhd正負 の 計算 最高のぬりえ




小学6年生 四則混合 分数 プラス パル



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料



1




正負の数の計算ー四則混合 無料で使える中学学習プリント




2桁の3つの掛け算と足し算と引き算 問題 184 400




正負の数の計算ー四則混合 無料で使える中学学習プリント




四則混合計算と分配法則 中学受験父さん



算数 小数分数四則混合計算 Z22g5q05kw 算数問題集のアキラストア 通販 Yahoo ショッピング
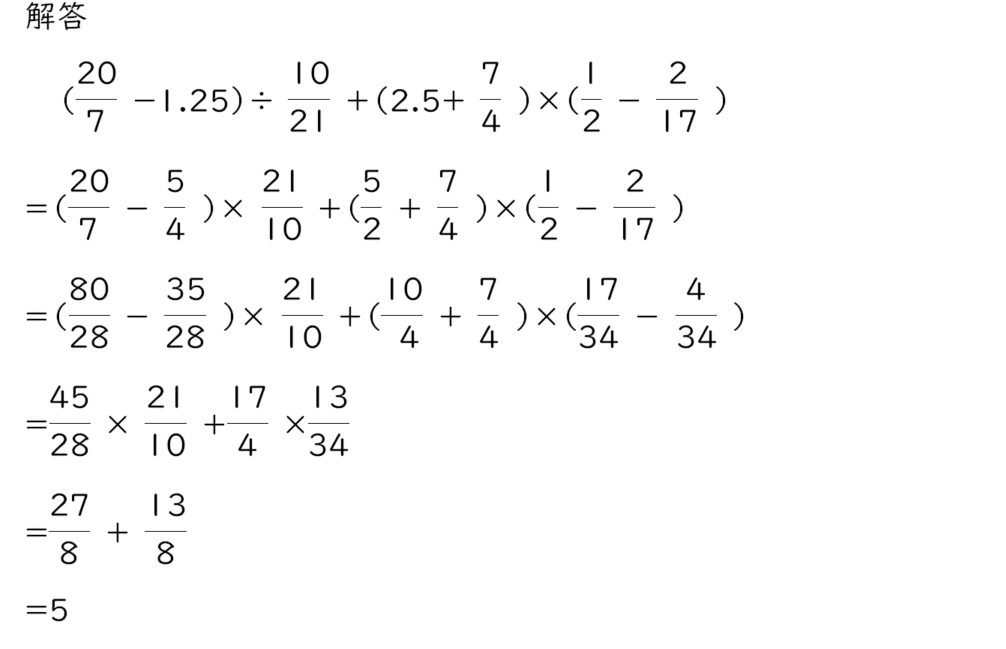



分数小数混合四則計算 芝 H19 大問1の1



四則混合計算の逆算のやり方を教えてください 子供に教えるやり方を Yahoo 知恵袋



1




累乗とかっこを含む四則計算
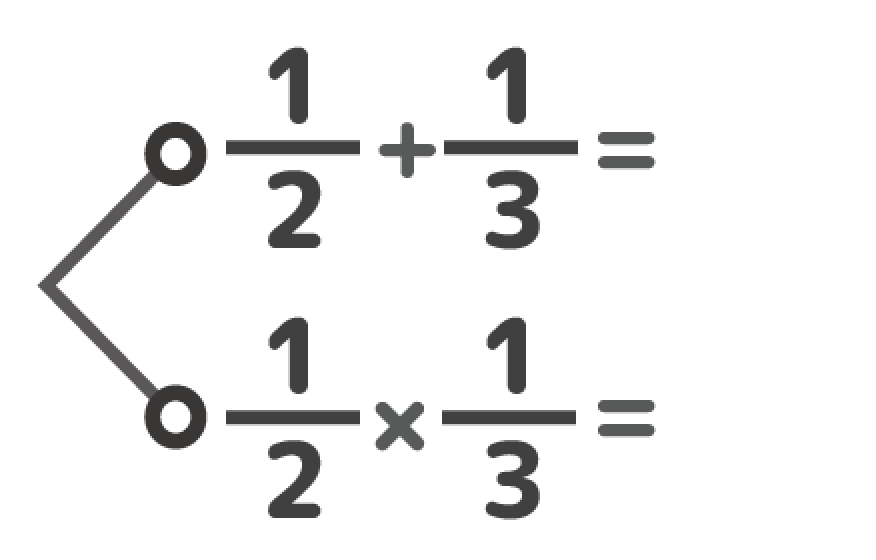



小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館




かみのドリル 自然数の四則混合と逆算 少しずつ増やしていくページ8




ルートの四則演算 計算する順番に注意しよう 中学や高校の数学の計算問題




高校入試突破 計算力トレーニング の評判や使い方まとめ 中学数学のおすすめ参考書紹介




正負の数の計算ー四則混合 無料で使える中学学習プリント




計算問題 編 Step1 複雑な計算は ルール を覚えれば解きやすくなる 中学受験 お父さんが教える算数 ダイヤモンド オンライン




四則混合計算 清水塾




中学数学1年 四則の混じった計算と分配法則による計算の工夫 受験の月




虫食い算 たし算2 算数ドリル 小学1 2生の挑戦 プラス パル




逆算の解き方 先に済ませる計算 カテキョウブログ
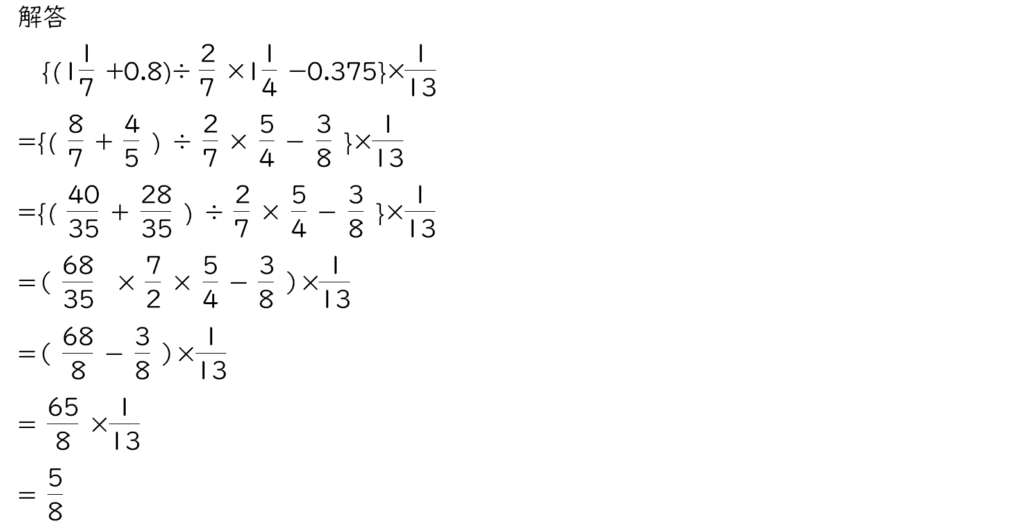



分数小数混合四則計算 女子学院 H12大問1の1



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
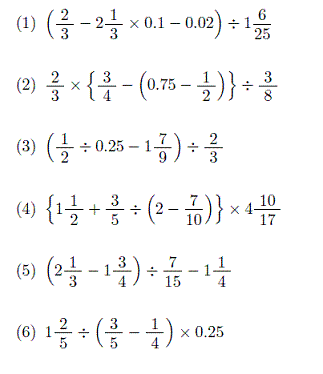



かみのドリル 入試類題 四則混合の計算ドリル




6 2 1 2 問題について教育委員会に問い合わせてみた 半月記




6 2 1 2 1 Or 9 まとめ Togetter



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料




小学生の算数 引き算 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生



四則混合算の解き方がわかりません解き方が載っておらず計算の仕方がわかりませ Yahoo 知恵袋




四則計算 ちびむすドリル 小学生



四則混合の計算問題に強くなろう 家庭で教える算数 中学受験ナビ




四則 Japaneseclass Jp
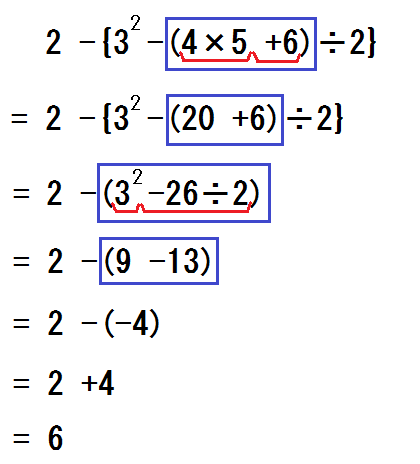



中学数学 正負の数 でつまずく原因と解決法 四則混合 分配法則
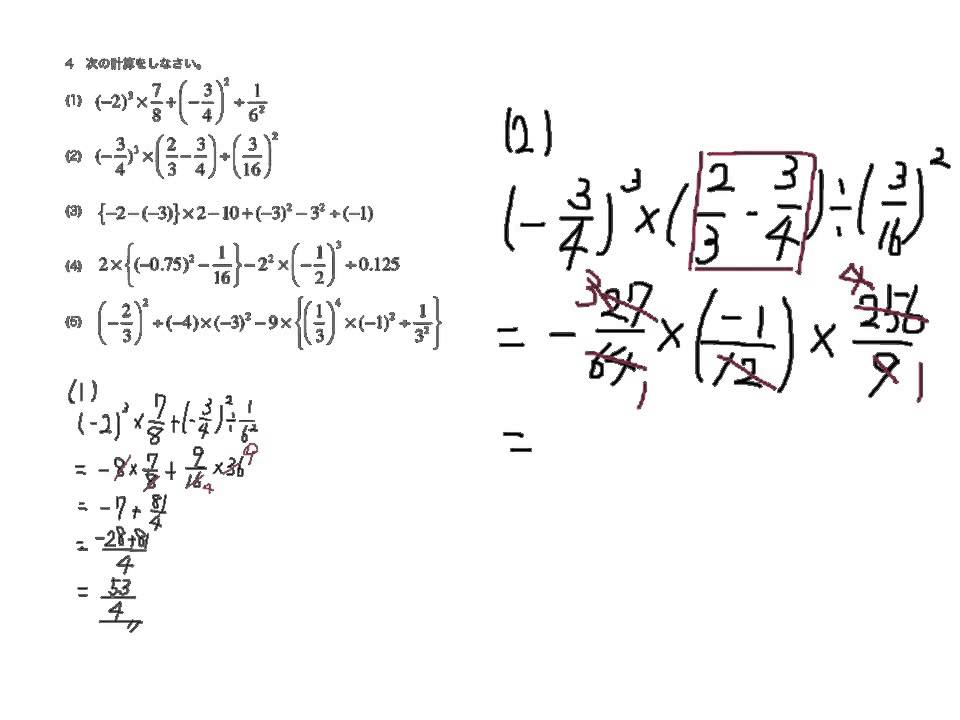



一章まとめ4 正の数 負の数 四則混合計算 難関 Youtube
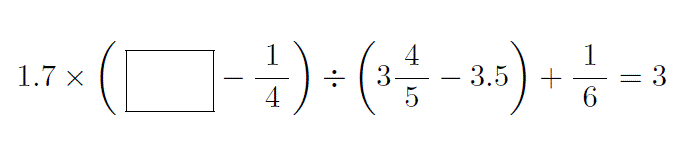



かみのドリル 中学受験 逆算 少しずつ増やしていくページ4




小学3年生 算数ドリル 分数2 分母が同じどうしのたし算 プラス パル



4年算数 式と計算の順じょ 教え方のポイント 2



中1 四則混合 分数まじりの計算 2016年度 Youtube




清水塾 ページ 12 清水塾




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ
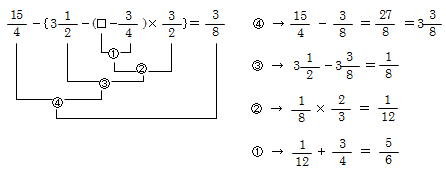



計算力の強化 前田昌宏の中学受験が楽しくなる算数塾




中学数学 正負の数の四則混合算を解いてみよう 日々是鍛錬 ひびこれたんれん



分数の計算ドリル




新着四則混合計算 小学生 最高のぬりえ




四則混合の計算問題 小学生向け 小学生 中学生の勉強




第26回 分数の計算 四則混合計算 逆算 5年生 日能研の歩き方




平方根 ルートの四則計算 ドリるーむ




文章問題で四則演算の理解度をチェックする 最先端家庭学習watch




平成27年度都立高入試問題 数学 大問 ー1 5 グッドタイムスクール



0 件のコメント:
コメントを投稿